今天在知乎上回答了这样一个问题:网上常能见到的一段JS随机数生成算法如下,为什么用9301, 49297, 233280这三个数字做基数?
问题中提到的代码如下:1
2
3
4
5
6
7
8
9
10
11
12function rnd( seed ){
seed = ( seed * 9301 + 49297 ) % 233280; //Magic!
return seed / ( 233280.0 );
};
function rand(number){
today = new Date();
seed = today.getTime();
return Math.ceil( rnd( seed ) * number );
};
myNum=(rand(5));
经过一系列的digging,最终找到了这个问题的答案,这三个数的选择是有数学依据的。
入门级的选择标准
这种随机数生成器叫做线性同余生成器(LCG, Linear Congruential Generator),几乎所有的运行库提供的rand都是采用的LCG,形如:
$I_{n+1}=aI_n + c\ (mod\ m)$
生成的随机数序列最大周期m,生成0到m-1之间的随机数。要达到这个最大周期,必须满足
- c与m互质
- a - 1可以被m的所有质因数整除
- 如果m是4的倍数,a - 1也必须是4的倍数
以上三条被称为Hull-Dobell定理。
作为一个随机数生成器,周期不够大是不好意思混的,所以这是要求之一。
可以看到,a=9301, c = 49297, m = 233280这组参数,以上三条全部满足。
进阶级的选择标准
要在随机数生成器界混,仅仅入门是不够的。
从工程的角度来讲,$(m - 1)a + c$的值要(在合理的范围内)足够小,以避免溢出的问题。
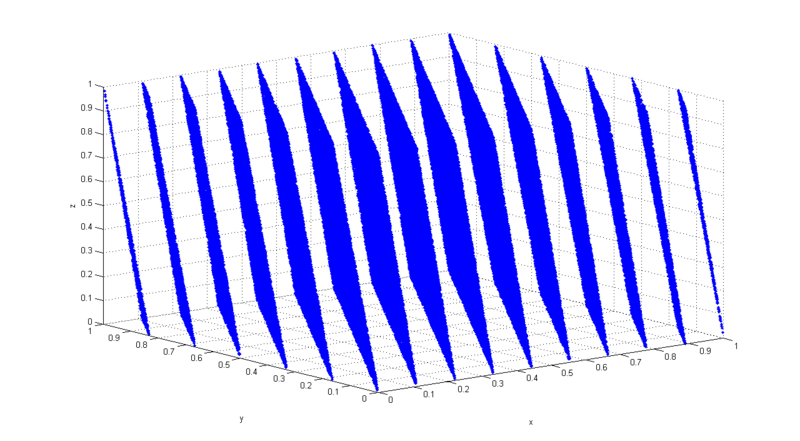
从安全(实用)性的角度来讲,还要满足良好的随机性,这一点可以通过Knunth’s Spectral Test来评估(见[2]),要通过2,3,4,5以及6维的Spectral Test才行。Spectral Test考察的就是生成的随机数序列在超空间的网格结构(lattice structure),当年IBM的RANDU子程序闹出的乌龙,连3维的Spectral Test就不能通过,上图嘲讽下:
其中每个点代表三个连续的RANDU生成的随机数值,可以看到所有随机数分布在了15个二维平面上。
在这种要求面前,c的值最好:
- 是质数 (c = 49297就是质数)
- 接近$(\frac{1}{2}-\frac{1}{6}\sqrt{3})m$,(m = 233280时为49297.86460172205)
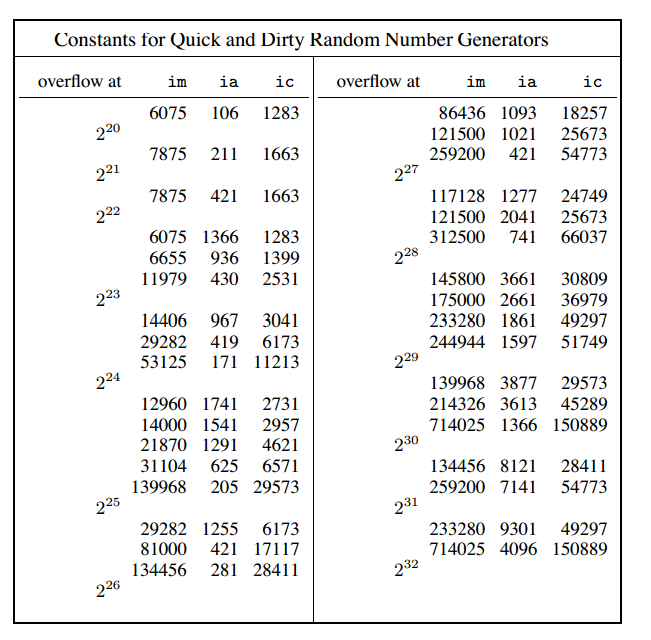
所以有了这样一些基本的标准,能够选择的参数范围就小了很多,弄个程序跑下Spectral Test,就能得到可选的参数组: